回転移動を行列で表す

図形が原点を中心にφ°だけ回転するとします。
こんな感じです。

図形の回転は要するに全ての点が同じ角度で回転したということです。なのである１点だけ考えれば良いのです。

上図は点Pがφ°回転してP'に移動した図です。これを見てみますと、新しい点でのx軸からの角度θ'は元の点の角度θと回転角φの足し算になっていることがわかります。

角度の足し算θ+φというのはどこかで見たことがありませんか？

これです。

加法定理に似ていますね。

回転というのは加法定理と同じなのです。加法定理を少し拡張して、原点からの距離rを追加したものだと考えていいでしょう。
そのため、回転移動を求めるには、加法定理を使うと簡単です。

まず、P、P'を極座標表示してみます。

このとき、P'はPからφ°回転した点なので、

となります。後はこれを直交座標表示に直します。極座標表示から直交座標表示に直すためには、

という計算をします。

ではx'、y'を直交座標表示に直してみます。途中で加法定理を用いています。

後はこれを行列表示します。

転置した場合、

はい、回転お終いです。

次は、回転の中心を指定した回転を考えてみます。
これはもちろん一回の変換でできるのですが、その行列は３つの変換行列をかけ算した行列になります。

回転の中心を指定した回転では、

１．回転の中心を原点に平行移動
２．回転
３．回転の中心を元の位置に平行移動

という３段階の手順をふみます。
よって変換はこうなります。

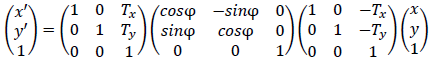
右から１、２、３の変換になっています。
この３つの変換をかけ算して１つにしてみます。

計算は簡単なので是非やってみてください。私が計算ミスしてるかもしれませんよ？
この行列が回転の中心を指定した回転を一回で行う変換です。
転置した場合も同じく

とすればＯＫです。